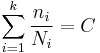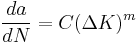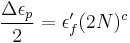Fatigue (material)
| Materials failure modes |
|---|
| Buckling |
| Corrosion |
| Creep |
| Fatigue |
| Fracture |
| Impact |
| Mechanical overload |
| Thermal shock |
| Wear |
| Yielding |
In materials science, fatigue is the progressive and localized structural damage that occurs when a material is subjected to cyclic loading. The nominal maximum stress values are less than the ultimate tensile stress limit, and may be below the yield stress limit of the material.
Fatigue occurs when a material is subjected to repeated loading and unloading. If the loads are above a certain threshold, microscopic cracks will begin to form at the surface. Eventually a crack will reach a critical size, and the structure will suddenly fracture. The shape of the structure will significantly affect the fatigue life; square holes or sharp corners will lead to elevated local stresses where fatigue cracks can initiate. Round holes and smooth transitions or fillets are therefore important to increase the fatigue strength of the structure.
Fatigue life
ASTM defines fatigue life, Nf, as the number of stress cycles of a specified character that a specimen sustains before failure of a specified nature occurs.[1]
One method to predict fatigue life of materials is the Uniform Material Law (UML).[2] UML was developed for fatigue life prediction of aluminum and titanium alloys by the end of 20th century and extended to high-strength steels.[3]
Characteristics of fatigue

- In metals and alloys, the process starts with dislocation movements, eventually forming persistent slip bands that nucleate short cracks.
- Fatigue is a stochastic process, often showing considerable scatter even in controlled environments.
- The greater the applied stress range, the shorter the life.
- Fatigue life scatter tends to increase for longer fatigue lives.
- Damage is cumulative. Materials do not recover when rested.
- Fatigue life is influenced by a variety of factors, such as temperature, surface finish, microstructure, presence of oxidizing or inert chemicals, residual stresses, contact (fretting), etc.
- Some materials (e.g., some steel and titanium alloys) exhibit a theoretical fatigue limit below which continued loading does not lead to failure.
- In recent years, researchers (see, for example, the work of Bathias, Murakami, and Stanzl-Tschegg) have found that failures occur below the theoretical fatigue limit at very high fatigue lives (109 to 1010 cycles). An ultrasonic resonance technique is used in these experiments with frequencies around 10–20 kHz.
- High cycle fatigue strength (about 103 to 108 cycles) can be described by stress-based parameters. A load-controlled servo-hydraulic test rig is commonly used in these tests, with frequencies of around 20–50 Hz. Other sorts of machines—like resonant magnetic machines—can also be used, achieving frequencies up to 250 Hz.
- Low cycle fatigue (typically less than 103 cycles) is associated with widespread plasticity in metals; thus, a strain-based parameter should be used for fatigue life prediction in metals and alloys. Testing is conducted with constant strain amplitudes typically at 0.01–5 Hz.
Timeline of early fatigue research history
- 1837: Wilhelm Albert publishes the first article on fatigue. He devised a test machine for conveyor chains used in the Clausthal mines.[4]
- 1839: Jean-Victor Poncelet describes metals as being tired in his lectures at the military school at Metz.
- 1842: William John Macquorn Rankine recognises the importance of stress concentrations in his investigation of railroad axle failures. The Versailles train crash was caused by axle fatigue.[5]
- 1843: Joseph Glynn reports on fatigue of axle on locomotive tender. He identifies the keyway as the crack origin.
- 1848: Railway Inspectorate report one of the first tyre failures, probably from a rivet hole in tread of railway carriage wheel. It was likely a fatigue failure.
- 1849: Eaton Hodgkinson is granted a small sum of money to report to the UK Parliament on his work in ascertaining by direct experiment, the effects of continued changes of load upon iron structures and to what extent they could be loaded without danger to their ultimate security.
- 1854: Braithwaite reports on common service fatigue failures and coins the term fatigue.[6]
- 1860: Systematic fatigue testing undertaken by Sir William Fairbairn and August Wöhler.
- 1870: Wöhler summarises his work on railroad axles. He concludes that cyclic stress range is more important than peak stress and introduces the concept of endurance limit.[4]
- 1903: Sir James Alfred Ewing demonstrates the origin of fatigue failure in microscopic cracks.
- 1910: O. H. Basquin proposes a log-log relationship for SN curves, using Wöhler's test data.
- 1945: A. M. Miner popularises A. Palmgren's (1924) linear damage hypothesis as a practical design tool.
- 1954: L. F. Coffin and S. S. Manson explain fatigue crack-growth in terms of plastic strain in the tip of cracks.
- 1961: P. C. Paris proposes methods for predicting the rate of growth of individual fatigue cracks in the face of initial scepticism and popular defence of Miner's phenomenological approach.
- 1968: Tatsuo Endo and M. Matsuiski devise the rainflow-counting algorithm and enable the reliable application of Miner's rule to random loadings.
- 1970: W. Elber elucidates the mechanisms and importance of crack closure in slowing the growth of a fatigue crack due to the wedging effect of plastic deformation left behind the tip of the crack.
High-cycle fatigue
Historically, most attention has focused on situations that require more than 104 cycles to failure where stress is low and deformation primarily elastic.
The S-N curve
In high-cycle fatigue situations, materials performance is commonly characterised by an S-N curve, also known as a Wöhler curve . This is a graph of the magnitude of a cyclical stress (S) against the logarithmic scale of cycles to failure (N).
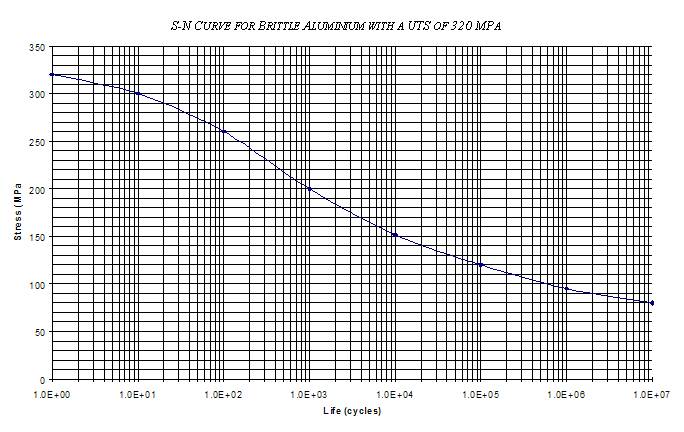
S-N curves are derived from tests on samples of the material to be characterised (often called coupons) where a regular sinusoidal stress is applied by a testing machine which also counts the number of cycles to failure. This process is sometimes known as coupon testing. Each coupon test generates a point on the plot though in some cases there is a runout where the time to failure exceeds that available for the test (see censoring). Analysis of fatigue data requires techniques from statistics, especially survival analysis and linear regression.
Probabilistic nature of fatigue
As coupons sampled from a homogeneous frame will manifest variation in their number of cycles to failure, the S-N curve should more properly be an S-N-P curve capturing the probability of failure after a given number of cycles of a certain stress. Probability distributions that are common in data analysis and in design against fatigue include the lognormal distribution, extreme value distribution, Birnbaum–Saunders distribution, and Weibull distribution.
Complex loadings
In practice, a mechanical part is exposed to a complex, often random, sequence of loads, large and small. In order to assess the safe life of such a part:
- Reduce the complex loading to a series of simple cyclic loadings using a technique such as rainflow analysis;
- Create a histogram of cyclic stress from the rainflow analysis;
- For each stress level, calculate the degree of cumulative damage incurred from the S-N curve; and
- Combine the individual contributions using an algorithm such as Miner's rule.
Miner's rule
In 1945, M. A. Miner popularised a rule that had first been proposed by A. Palmgren in 1924. The rule, variously called Miner's rule or the Palmgren-Miner linear damage hypothesis, states that where there are k different stress magnitudes in a spectrum, Si (1 ≤ i ≤ k), each contributing ni(Si) cycles, then if Ni(Si) is the number of cycles to failure of a constant stress reversal Si, failure occurs when:
C is experimentally found to be between 0.7 and 2.2. Usually for design purposes, C is assumed to be 1.
This can be thought of as assessing what proportion of life is consumed by stress reversal at each magnitude then forming a linear combination of their aggregate.
Though Miner's rule is a useful approximation in many circumstances, it has several major limitations:
- It fails to recognise the probabilistic nature of fatigue and there is no simple way to relate life predicted by the rule with the characteristics of a probability distribution. Industry analysts often use design curves, adjusted to account for scatter, to calculate Ni(Si).
- There is sometimes an effect in the order in which the reversals occur. In some circumstances, cycles of low stress followed by high stress cause more damage than would be predicted by the rule. It does not consider the effect of overload or high stress which may result in a compressive residual stress. High stress followed by low stress may have less damage due to the presence of compressive residual stress.
Paris' Relationship
Anderson, Gomez and Paris derived relationships for the stage II crack growth with cycles N, in terms of the cyclical component ΔK of the Stress Intensity Factor K[7]
where a is the crack length and m is typically in the range 3 to 5 (for metals).
This relationship was later modified (by Forman, 1967[8]) to make better allowance for the mean stress, by introducing a factor depending on (1-R) where R = min. stress/max stress, in the denominator.
Low-cycle fatigue
Where the stress is high enough for plastic deformation to occur, the account in terms of stress is less useful and the strain in the material offers a simpler description. Low-cycle fatigue is usually characterised by the Coffin-Manson relation (published independently by L. F. Coffin in 1954 and S. S. Manson 1953):
-where:
- Δεp /2 is the plastic strain amplitude;
- εf' is an empirical constant known as the fatigue ductility coefficient, the failure strain for a single reversal;
- 2N is the number of reversals to failure (N cycles);
- c is an empirical constant known as the fatigue ductility exponent, commonly ranging from -0.5 to -0.7 for metals in time independent fatigue. Slopes can be considerably steeper in the presence of creep or environmental interactions.
A similar relationship for materials such as Zirconium, used in the nuclear industry.[9]
Fatigue and fracture mechanics
The account above is purely empirical and, though it allows life prediction and design assurance, life improvement or design optimisation can be enhanced using fracture mechanics. It can be developed in four stages.
- Crack nucleation;
- Stage I crack-growth;
- Stage II crack-growth; and
- Ultimate ductile failure.
Factors that affect fatigue-life
- Cyclic stress state: Depending on the complexity of the geometry and the loading, one or more properties of the stress state need to be considered, such as stress amplitude, mean stress, biaxiality, in-phase or out-of-phase shear stress, and load sequence,
- Geometry: Notches and variation in cross section throughout a part lead to stress concentrations where fatigue cracks initiate.
- Surface quality. Surface roughness cause microscopic stress concentrations that lower the fatigue strength. Compressive residual stresses can be introduced in the surface by e.g. shot peening to increase fatigue life. Such techniques for producing surface stress are often referred to as peening, whatever the mechanism used to produce the stress. laser peening and ultrasonic impact treatment can also produce this surface compressive stress and can increase the fatigue life of the component. This improvement is normally observed only for high-cycle fatigue.
- Material Type: Fatigue life, as well as the behavior during cyclic loading, varies widely for different materials, e.g. composites and polymers differ markedly from metals.
- Residual stresses: Welding, cutting, casting, and other manufacturing processes involving heat or deformation can produce high levels of tensile residual stress, which decreases the fatigue strength.
- Size and distribution of internal defects: Casting defects such as gas porosity, non-metallic inclusions and shrinkage voids can significantly reduce fatigue strength.
- Direction of loading: For non-isotropic materials, fatigue strength depends on the direction of the principal stress.
- Grain size: For most metals, smaller grains yield longer fatigue lives, however, the presence of surface defects or scratches will have a greater influence than in a coarse grained alloy.
- Environment: Environmental conditions can cause erosion, corrosion, or gas-phase embrittlement, which all affect fatigue life. Corrosion fatigue is a problem encountered in many aggressive environments.
- Temperature: Higher temperatures generally decrease fatigue strength.
Design against fatigue
Dependable design against fatigue-failure requires thorough education and supervised experience in structural engineering, mechanical engineering, or materials science. There are three principal approaches to life assurance for mechanical parts that display increasing degrees of sophistication:
- Design to keep stress below threshold of fatigue limit (infinite lifetime concept);
- Design (conservatively) for a fixed life after which the user is instructed to replace the part with a new one (a so-called lifed part, finite lifetime concept, or "safe-life" design practice);
- Instruct the user to inspect the part periodically for cracks and to replace the part once a crack exceeds a critical length. This approach usually uses the technologies of nondestructive testing and requires an accurate prediction of the rate of crack-growth between inspections. This is often referred to as damage tolerant design or "retirement-for-cause".
Stopping fatigue
Fatigue cracks that have begun to propagate can sometimes be stopped by drilling holes, called drill stops, in the path of the fatigue crack.[10] This is not recommended as a general practice because the hole represents a stress concentration factor which depends on the size of the hole and geometry. There is thus the possibility of a new crack starting in the side of the hole. It is always far better to replace the cracked part entirely.
Material change
Changes in the materials used in parts can also improve fatigue life. For example, parts can be made from better fatigue rated metals. Complete replacement and redesign of parts can also reduce if not eliminate fatigue problems. Thus helicopter rotor blades and propellers in metal are being replaced by composite equivalents. They are not only lighter, but also much more resistant to fatigue. They are more expensive, but the extra cost is amply repaid by their greater integrity, since loss of a rotor blade usually leads to total loss of the aircraft. A similar argument has been made for replacement of metal fuselages, wings and tails of aircraft.
Infamous fatigue failures
Versailles train crash

Following the King's fete celebrations at the Palace of Versailles, a train returning to Paris crashed in May 1842 at Meudon after the leading locomotive broke an axle. The carriages behind piled into the wrecked engines and caught fire. At least 55 passengers were killed trapped in the carriages, including the explorer Jules Dumont d'Urville. This accident is known in France as the "Catastrophe ferroviaire de Meudon". The accident was witnessed by Joseph Locke, the famous British locomotive engineer, and widely reported in Britain. It was discussed extensively by engineers, who sought an explanation.
The derailment had been the result of a broken locomotive axle. Rankine's investigation of broken axles in Britain highlighted the importance of stress concentration, and the mechanism of crack growth with repeated loading. His and other papers suggesting a crack growth mechanism through repeated stressing, however, were ignored, and fatigue failures occurred at an ever increasing rate on the expanding railway system. Other and spurious theories seemed to be more acceptable, such as the idea that the metal had somehow "crystallized". The notion was based on the crystalline appearance of the fast fracture region of the crack surface, but ignored the fact that the metal was already highly crystalline.
De Havilland Comet

Metal fatigue became apparent to aircraft engineers in 1954 after three de Havilland Comet passenger jets had broken up in mid-air and crashed within a single year. Systematic tests were conducted on a fuselage in a water tank. After the equivalent of 3,000 flights investigators at the RAE were able to conclude that the crash had been due to failure of the pressure cabin at the forward ADF window in the roof. This 'window' was in fact one of two apertures for the aerials of an electronic navigation system in which opaque fibreglass panels took the place of the window 'glass'. The failure was a result of metal fatigue caused by the repeated pressurisation and de-pressurisation of the aircraft cabin. Another fact was that the supports around the windows were riveted, not glued, as the original specifications for the aircraft had called for. The problem was exacerbated by the punch rivet construction technique employed. Unlike drill riveting, the imperfect nature of the hole created by punch riveting caused manufacturing defect cracks which may have caused the start of fatigue cracks around the rivet. The investigators examined the final piece of wreckage with a regular microscope.
The Comet's pressure cabin had been designed to a safety factor comfortably in excess of that required by British Civil Airworthiness Requirements (2.50 × P as opposed to the requirement of 1.33 × P and an ultimate load of 2.00 × P, P being the cabin proof pressure) and the accident caused a revision in the estimates of the safe loading strength requirements of airliner pressure cabins.
In addition, it was discovered that the stresses around pressure cabin apertures were considerably higher than had been anticipated, especially around sharp-cornered cut-outs, such as windows. As a result, future jet airliners would feature windows with rounded corners, the curve eliminating a stress concentration. This was a noticeable distinguishing feature of all later models of the Comet.Investigators from the Royal Aircraft Establishment at Farnborough in England told a public enquiry that the sharp corners near the plane's window openings acted as initiation sites for cracks. The skin of the aircraft was also too thin, and cracks from manufacturing stresses were present at the corners. All aircraft windows were immediately redesigned with rounded corners.
The 1980 capsize of the oil platform Alexander L. Kielland

The Alexander L. Kielland was a Norwegian semi-submersible drilling rig that capsized whilst working in the Ekofisk oil field in March 1980 killing 123 people. The capsize was the worst disaster in Norwegian waters since World War II. The rig, located approximately 320 km east from Dundee, Scotland, was owned by the Stavanger Drilling Company of Norway and was on hire to the U.S. company Phillips Petroleum at the time of the disaster. In driving rain and mist, early in the evening of 27 March 1980 more than 200 men were off duty in the accommodation on the Alexander L. Kielland. The wind was gusting to 40 knots with waves up to 12 m high. The rig had just been winched away from the Edda production platform. Minutes before 18:30 those on board felt a 'sharp crack' followed by 'some kind of trembling'. Suddenly the rig heeled over 30° and then stabilised. Five of the six anchor cables had broken, the one remaining cable preventing the rig from capsizing. The list continued to increase and at 18.53 the remaining anchor cable snapped and the rig turned upside down.
A year later in March 1981, the investigative report[12] concluded that the rig collapsed owing to a fatigue crack in one of its six bracings (bracing D-6), which connected the collapsed D-leg to the rest of the rig. This was traced to a small 6 mm fillet weld which joined a non-load-bearing flange plate to this D-6 bracing. This flange plate held a sonar device used during drilling operations. The poor profile of the fillet weld contributed to a reduction in its fatigue strength. Further, the investigation found considerable amounts of lamellar tearing in the flange plate and cold cracks in the butt weld. Cold cracks in the welds, increased stress concentrations due to the weakened flange plate, the poor weld profile, and cyclical stresses (which would be common in the North Sea), seemed to collectively play a role in the rig's collapse.
Others
- United Airlines Flight 232, Japan Airlines Flight 123, China Airlines Flight 611, Los Angeles Airways Flight 417, and El Al Flight 1862
- The 1957 plane crash of the "Mt. Pinatubo", presidential plane of Philippine President Ramon Magsaysay who died in the crash along with 24 others.
- The 1985 Japan Airlines Flight 123 crash after the aircraft lost its tail. It was was caused by fatigue from a faulty repair to the rear bulkhead
- The 1919 Boston Molasses Disaster has been attributed to a fatigue failure
- The 1998 Eschede train disaster (crash of an InterCityExpress train) caused by fatigue of a single composite wheel
- The 2002 loss of China Airlines Flight 611
- The 2005 crash of Chalk's Ocean Airways Flight 101
See also
- Air safety
- Embedment
- Fatigue_limit
- Fracture mechanics
- Forensic engineering
- Forensic materials engineering
- Fractography
- Kalitta Air
- Materials science
- Shock (mechanics)
- Structural failure
- Ultrasonic Impact Treatment
- Vibration
References
- ↑ Stephens, Ralph I.; Fuchs, Henry O. (2001). Metal Fatigue in Engineering (Second edition ed.). John Wiley & Sons, Inc.. p. 69. ISBN 0-471-51059-9.
- ↑ A. Bäumel, Jr and T. Seeger (1990). Materials data for cyclic loading, supplement 1. Elsevier. ISBN 978-0444886033.
- ↑ S. Korkmaz (2010). Uniform Material Law: Extension to High-Strength Steels. VDM. ISBN 978-3-639-25625-3.
- ↑ 4.0 4.1 W. Schutz (1996). A history of fatigue. Engineering Fracture Mechanics 54: 263-300. DOI
- ↑ W.J.M. Rankine. (1842). "On the causes of the unexpected breakage of the journals of railway axles, and on the means of preventing such accidents by observing the law of continuity in their construction". Institution of Civil Engineers, Minutes of Proceedings, 105-108.
- ↑ F. Braithwaite. (1854). "On the fatigue and consequent fracture of metals". Institution of Civil Engineers, Minutes of Proceedings, 463–474.
- ↑ P. C. Paris, M. P. Gomez and W. E. Anderson. A rational analytic theory of fatigue. The Trend in Engineering (1961). 13, 9-14.
- ↑ [1]
- ↑ O'Donnell, W.J. and B. F. Langer. Nuclear Science and Engineering, Vol 20, pp. 1-12, 1964.
- ↑ Material Technologies, Inc. Completes EFS Inspection of Bridge in New Jersey Press release regarding metal fatigue damage to the Manahawkin Bay Bridge in New Jersey
- ↑ "ObjectWiki: Fuselage of de Havilland Comet Airliner G-ALYP". Science Museum. 24 September 2009. http://objectwiki.sciencemuseum.org.uk/wiki/Fuselage_of_de_Havilland_Comet_Airliner_G-ALYP. Retrieved 9 October 2009.
- ↑ The Alexander L. Kielland accident, Report of a Norwegian public commission appointed by royal decree of March 28, 1980, presented to the Ministry of Justice and Police March, 1981 ISBN B0000ED27N
Further reading
- Andrew, W. (1995) Fatigue and Tribological Properties of Plastics and Elastomers, ISBN 1-884207-15-4
- Dieter, G. E. (1988) Mechanical Metallurgy, ISBN 0-07-100406-8
- Little, R. E. & Jebe, E. H. (1975) Statistical design of fatigue experiments ISBN 0-470-54115-6
- A. G. Palmgren (1924): Die Lebensdaur von Kugellagern (Life Length of Roller Bearings. In German). Zeitschrift des Vereines Deutscher Ingenieure (VDI Zeitschrift), ISSN 0341-7258, Vol 68, No 14, April 1924, pp 339-341.
- Schijve, J. (2009). Fatigue of Structures and Materials, 2nd Edition with Cd-Rom. Springer. ISBN 978-1-4020-6807-2.
- Lalanne, C. (2009). Fatigue Damage. ISTE - Wiley. ISBN 978-1-84821-125-4.
- Pook, Les (2007). Metal Fatigue, What it is, why it matters. Springer. ISBN 978-1-4020-5596-6.
- Draper, John (2008). Modern Metal Fatigue Analysis. EMAS. ISBN 0-947817-79-4.